Plotte med Python
Contents
Plotte med Python¶
Vi kan plotte diagrammer og grafer med Python. Da bruker vi ofte modulen matplotlib.pyplot. Vi imorterer denne og lager et alias (en forkortelse) slik:
import matplotlib.pyplot as plt
Vi viser hvordan vi kan gjøre de ulike plottene gjennom en del eksempler.
Linjediagrammer¶
Eksempel 1¶
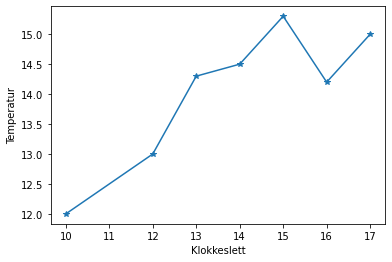
Tabellen nedenfor viser temperaturen for noen klokkeslett.
Kokkeslett |
10 |
12 |
13 |
14 |
15 |
16 |
17 |
|---|---|---|---|---|---|---|---|
Temperatur \(^\circ C\) |
12 |
13 |
14.3 |
14.5 |
15.3 |
14.2 |
15.0 |
Plott tallen i tabellen.
# Vi lager to lister, en for x-verdier og en for y-verdier:
Klokkeslett = [10, 12, 13, 14, 15, 16, 17]
Temperatur = [12, 13, 14.3, 14.5, 15.3, 14.2, 15]
plt.plot(Klokkeslett, Temperatur, "-*")
plt.xlabel('Klokkeslett')
plt.ylabel('Temperatur')
plt.show()
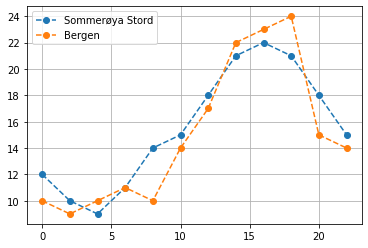
Eksempel 2¶
Lag en grafisk representasjon av tallene i tabellen:
Klokkeslett |
0.00 |
2.00 |
4.00 |
6.00 |
8.00 |
10.00 |
12.00 |
14.00 |
16.00 |
18.00 |
20.00 |
22.00 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
Temperatur Leirvik |
12 |
10 |
9 |
11 |
14 |
15 |
18 |
21 |
22 |
21 |
18 |
15 |
Temperatur Bergen |
10 |
9 |
10 |
11 |
10 |
14 |
17 |
22 |
23 |
24 |
15 |
14 |
import matplotlib.pyplot as plt
Tid = list(range(0, 23, 2))
TempLeirvik = [12, 10, 9, 11, 14, 15, 18, 21, 22, 21, 18, 15]
TempBergen = [10, 9, 10, 11, 10, 14, 17, 22, 23, 24, 15, 14]
plt.plot(Tid, TempLeirvik, "o--", label="Sommerøya Stord")
plt.plot(Tid, TempBergen, "o--", label="Bergen")
plt.legend()
plt.grid()
plt.show()
Plotting av kontinuerlige funksjoner¶
Dersom vi skal plotte kontinuerlige funksjoner, må vi lage mange x-verdier som vi kan bruke. For å lage y-verdien definerer vi funksjonen og finner y-verdiene tilhørende hver x-verdi. Dersom vi bruker numpy er dette ganske greit å gjøre.
Eksempel 3¶
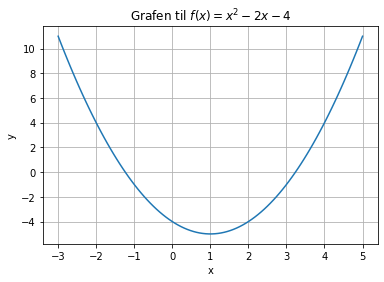
Plott grafen til \(f(x)=x^2-2x-4\) i et koordinatsystem. Velg x-verdier mellom \(-3\) og \(5\).
import matplotlib.pyplot as plt # For å kunne plotte
import numpy as np # For å kunne lage en x-verdier og y-verdier
# Definerer funksjonen:
def f(x):
return x**2-2*x-4
# definerer x-verdier og y-verdier
X = np.linspace(-3, 5, 100) # 100 x-verdier mellom -3 og 5
Y = f(X) # 100 y-verdier
plt.plot(X, Y) # Plotter x-verdier og y-verdier
plt.xlabel("x") # Legger til navn på x-aksen
plt.ylabel("y") # Legger til navn på y-aksen
plt.title(f"Grafen til $f(x)=x^2-2x-4$") # Legger til tittel
plt.grid() # Legger til rutenett på grafen
plt.show()
Eksempel 4¶
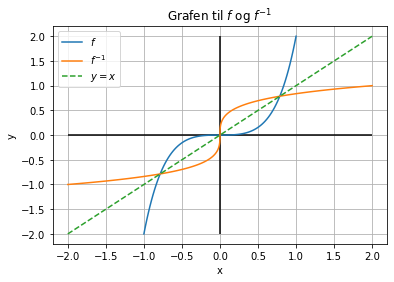
Funksjonen \(f\) er gitt ved
Tegn grafen til \(f\) sammen med grafen til den omvendte funksjonen \(f ^ {-1}\) i samme koordinatsystem.
import numpy as np
import matplotlib.pyplot as plt
X = np.linspace(-1, 1, 100)
def f(x):
return x**5+x**3
Y = f(X)
plt.plot(X, Y, label=r"$f$")
plt.plot(Y, X, label=r"$f^{-1}$")
plt.plot([-2, 2], [-2, 2],"--", label=r"$y=x$")
plt.hlines(0, -2, 2)
plt.vlines(0, -2, 2)
plt.title(r"Grafen til $f$ og $f^{-1}$")
plt.xlabel("x")
plt.ylabel("y")
plt.grid()
plt.legend()
plt.show()
Eksempel 5¶
Funksjonen \(f\) er gitt ved
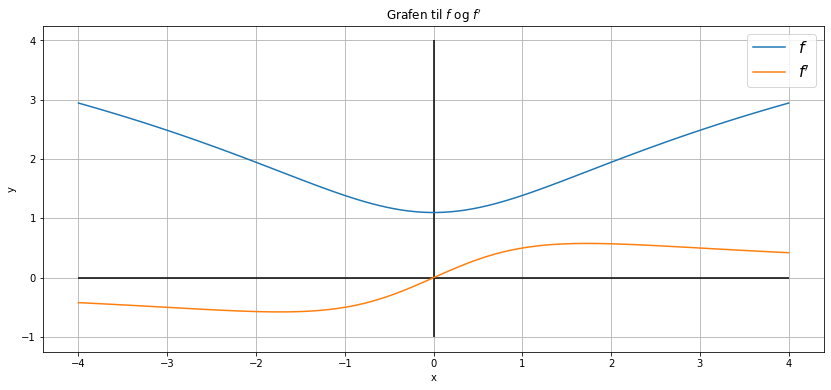
Tegn grafen til \(f\) og grafen til \(f'\) i et koordinatsystem.
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return np.log(x**2+3) # np.log(x) er naturlig logaritme til x
# Derfinerer den deriverte til funksjonen f:
def df(x, h=0.00001):
return (f(x+h)-f(x))/h
# Definerer x-verdier og y-verdier:
X = np.linspace(-4, 4, 100)
Y = f(X)
dY = df(X)
plt.figure(figsize=(14, 6)) # Definerer størrelse på figur
plt.plot(X, Y, label=r"$f$")
plt.plot(X, dY, label=r"$f'$")
plt.vlines(0, -1, 4) # Legger til y-aksen
plt.hlines(0, -4, 4) # Legger til x-aksen
plt.xlabel("x")
plt.ylabel("y")
plt.title(r"Grafen til $f$ og $f'$")
plt.grid()
plt.legend(fontsize=16)
plt.show()