Løsningsforslag til utvalgte oppgaver i kapittel 5#
Oppgave 5.1#
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return 2**x -3+2*x # Jeg ønsker å finne nullpunktet til denne funksjonen
# Plotter først grafen for å få et inntrykk av funksjonen:
X = np.linspace(-2,2,100) # Lager en liste med 100 punkter mellom -10 og 10
Y = f(X) # Beregner funksjonsverdiene for disse punktene
plt.plot(X,Y) # Plotter funksjonen
plt.grid() # Viser et rutenett
plt.show() # Viser grafen
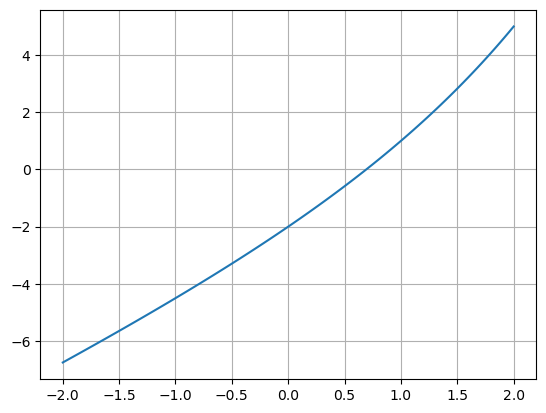
Siden jeg vet at \(f(x)\) er strengt voksende, så er det kun ett nullpunkt. Jeg ser at dette ligger mellom 0 og 1.
X = np.linspace(0,1,1000) # Lager en array med 1000 punkter mellom 0 og 1
Y = f(X) # Beregner funksjonsverdiene for disse punktene
for i in range(len(X)-1):
if Y[i]*Y[i+1] < 0: # Dersom produktet av funksjonsverdiene er negativt, er det et nullpunkt
print(f"Nullpunkt: mellom {X[i]:.3f} og {X[i+1]:.3f}")
Nullpunkt: mellom 0.692 og 0.693
Oppgave 5.2#
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return x**3 -3*x**2+1 # Jeg ønsker å finne nullpunktet til denne funksjonen
# Plotter først grafen for å få et inntrykk av funksjonen:
X = np.linspace(-2,4,100) # Lager en liste med 100 punkter mellom -10 og 10
Y = f(X) # Beregner funksjonsverdiene for disse punktene
plt.plot(X,Y) # Plotter funksjonen
plt.grid() # Viser et rutenett
plt.show() # Viser grafen
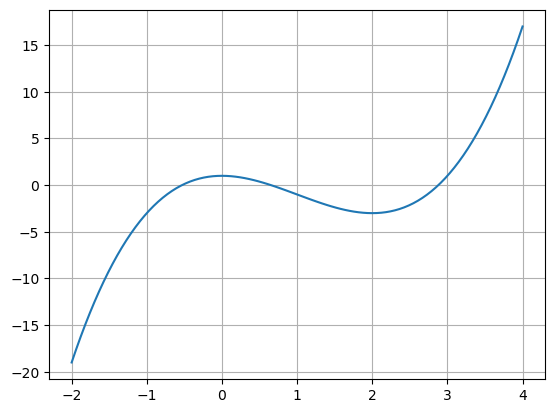
Jeg ser at det er tre nullpunkter. Ett mellom -1 og 0, ett mellom 0 og 1 og ett mellom 2 og 3. Siden hver at de tre intervallene jeg skal bruke har lengde 1, så må jeg bruke 34 iterasjoner.
For hver iterasjon halverer jeg intervallet, så jeg trenger 34 iterasjoner.
def f(x):
return x**3 -3*x**2+1 # Jeg ønsker å finne nullpunktet til denne funksjonen
def halvering(a,b,epsilon):
""" Halveringsmetoden for å finne nullpunktet til en funksjon f(x)
i intervallet [a,b] med ønsket nøyaktighet epsilon.
"""
while b-a > epsilon:
m = (a+b)/2
if f(a)*f(m) < 0:
b = m
else:
a = m
return (a+b)/2
# Finner det første nullpunktet:
print(format(halvering(-1,0,1e-10),"0.10f"), end=", ")
# Finner det andre nullpunktet:
print(format(halvering(0,1,1e-10),"0.10f"), end=" og ")
# Finner det tredje nullpunktet:
print(format(halvering(2,3,1e-10),"0.10f"))
-0.5320888862, 0.6527036447 og 2.8793852416
Oppgave 5.3#
Her er et eksempel på en funksjon som ikke har et fikspunkt: \(f(x) = x^2 +1\). Denne vil aldri krysse linjen \(y=x\).
Funksjonen \(f(x) = x^2 +x -4\) har et fikspunkt i \(x=2\) og i \(x=-2\).
Oppgave 5.4#
Her kan vi ta utgangspunkt i \(f(x)=x(x-1)(x+1) = x^3 - x\). Vi ser at \(f(x)=0\) hvis og bare hvis \(x^3 = x\). Altså har \(g(x) = x^3\) et fikspunkt i \(x=0\), i \(x=1\) og i \(x=-1\).
Oppgave 5.5#
from numpy import cos
def f(x):
return cos(x) - x
x = 0 # Startverdien for x
epsilon = 1e-10 # Nøyaktigheten vi ønsker
while abs(f(x)) > epsilon:
x = cos(x)
print(f"{x:.10f}")
0.7390851332
Oppgave 5.6#
from numpy import sqrt
x = -1 # Startverdien for x
epsilon = 1e-10 # Nøyaktigheten vi ønsker
while abs(x -(-sqrt((1-x)/3))) > epsilon:
x = -sqrt((1-x)/3)
print(f"{x:.10f}")
-0.7675918794
Oppgave 5.7#
a)
import numpy as np
def f(x):
return np.exp(-x)
x=1
e = 1e-10
while abs(f(x) - x) > e:
x = f(x)
print(f"{x:.10f}")
0.5671432905
b)
def g(x):
return 1/(2+x**2)
x=1
e = 1e-10
while abs(g(x) - x) > e:
x = g(x)
print(f"{x:.10f}")
0.4533976516
Vi ser at dette er den eneste løsningen ved å plotte grafene til \(g(x)\) og \(h(x)=x\) i et koodinatsystem:
import matplotlib.pyplot as plt
import numpy as np
X = np.linspace(-3, 3, 1000)
plt.plot(X, g(X))
plt.plot(X, X)
plt.ylim(-1, 1)
plt.grid()
plt.show()
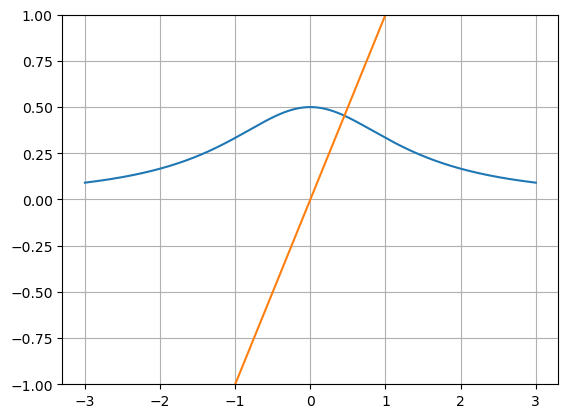
Oppgave 5.9#
Her kan vi ikke bruke \(f(x)=\tan x\) siden funksjonsverdiene ikke vil havne i intervallet \(\left<\frac{\pi}{2},\frac{3\pi}{2}\right>\). Vi må i stedet bruke den omvendte funksjonen \(f(x)=\arctan x\). Problemet med denne, er at den gir oss verdier mellom \(\left<-\frac{\pi}{2},\frac{\pi}{2}\right>\), og vi ønsker å finne verdier mellom \(\left<\frac{\pi}{2},\frac{3\pi}{2}\right>\). Vi kan løse dette ved å bruke \(f(x)=\pi + \arctan x\).
from numpy import arctan, pi
def f(x):
return pi + arctan(x)
x = 2 # Startverdien for x
epsilon = 1e-10 # Nøyaktigheten vi ønsker
while abs(f(x) - x) > epsilon:
x = f(x)
print(f"{x:.10f}")
4.4934094579
Oppgave 5.10#
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return x**3 -x**2+3
def g(x):
return 3*x**2 -2*x
N = 50
X = np.linspace(0,1,N) # Lager en liste med 100 punkter mellom 0 og 1
h = X[1]-X[0] # Beregner delta x
def df(x):
return (f(x+h)-f(x))/h
def df2(x):
return (f(x)-f(x-h))/h
def df3(x):
return (f(x+h)-f(x-h))/(2*h)
plt.figure(figsize=(10,3))
plt.subplot(1,3,1)
plt.plot(X,df(X), ".")
plt.plot(X,g(X), color="red")
plt.title(r"$D_+ f$ med n=50")
plt.subplot(1,3,2)
plt.plot(X,df2(X), ".")
plt.plot(X,g(X), color="red")
plt.title(r"$D_- f(x)$ med n=50")
plt.subplot(1,3,3)
plt.plot(X,df3(X), ".")
plt.plot(X,g(X), color="red")
plt.title(r"$D_0 f(x)$ med n=50")
plt.tight_layout()
plt.show()
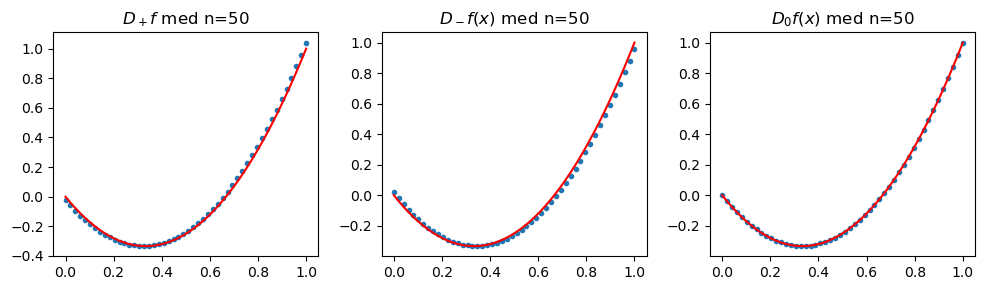
Oppgave 5.11#
a)
import numpy as np
import matplotlib.pyplot as plt
X = np.linspace(-2,2,1000) # Lager en liste med 1000 punkter mellom -2 og 2
def f(x):
return x**5+x-1 # Jeg ønsker å finne nullpunktet til denne funksjonen
plt.plot(X,f(X)) # Plotter funksjonen
plt.grid() # Viser et rutenett
plt.show() # Viser grafen
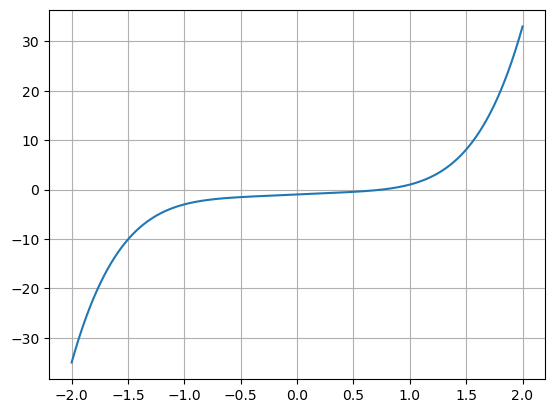
Jeg ser at \(f\) kun har ett nullpunkt. Dette ligger mellom 0 og 1. Jeg kunne også se at det er kun ett nullpunkt ved å observere at \(f'(x)=5x^4+1\). Denne er alltid større enn 0, og dermed er \(f\) alltid voksende.
def df(x, h=0.0001):
return (f(x+h)-f(x))/h # Derivasjonen av funksjonen
def newton(f, x0, epsilon):
""" Newtons metode for å finne nullpunktet til en funksjon f(x)
med ønsket nøyaktighet epsilon.
"""
def df(x, h= 0.00001):
return (f(x+h)-f(x))/h
while abs(f(x0)) > epsilon:
x0 = x0 - f(x0)/df(x0)
return x0
print(format(newton(f, 0.5,1e-10),"0.10f"))
0.7548776663
b) Tegner først grafen til \(f(x)=5\cdot \sqrt{x}-x-1\) i et koordinatsystem, slik at jeg kan se hvor det eventuelt er løsninger.
def f(x):
return 4*np.sqrt(x)-x-1 # Jeg ønsker å finne nullpunktet til denne funksjonen
X = np.linspace(0, 20, 1000)
plt.plot(X, f(X))
plt.grid()
plt.show()
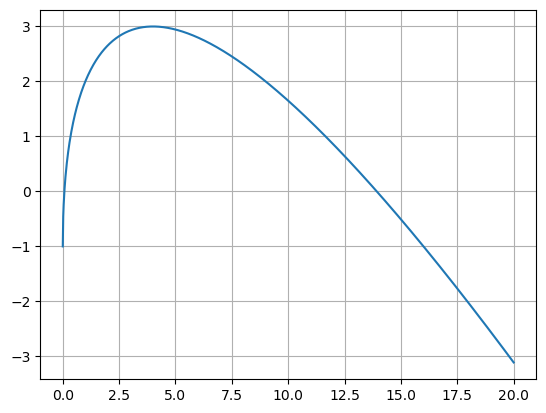
# Kan nå bruke Newtons metode for å finne nullpunktene. Det er to stk. Jeg må velge ulike startverdier for å finne begge:
print(format(newton(f, 0,1e-10),"0.10f"), end=", ") # startverdi 0
print(format(newton(f, 10,1e-10),"0.10f"), end=", ") # startverdi 10
0.0717967697, 13.9282032303,
Merk!
Merk at vi måtte starte til venstre for det første nullpunktet. Ellers ville tangenten ha ledet oss mot negative x-verdier og vi ville fått en feilmelding. Vi kan nemlig ikke ta kvadratroten av negative tall når vi jobbber med reelle tall.
Oppgave 5.13#
N = 1000
start = 0
slutt = 2
Dx = (slutt-start)/N # Bredden (eller høyden på trapesene)
def f(x):
return x**3
S = 1/2*Dx*(f(start)+f(slutt)) # Denne skal bli integralet
for i in range(1, N):
S = S + Dx*f(start + i* Dx)
print("Integralet er", format(S, ".4f") )
Integralet er 4.0000
Oppgave 5.14#
import numpy as np
N = 100
def f(x):
return np.sin(x)
X = np.linspace(0, np.pi, N)
h = X[1]-X[0] # Regner ut bredden på intervallene
S = h/3*(f(0)+f(np.pi)) # Tar med "endene"
for i in range(2, N, 2): # Legger til "partallsindekser":
S = S + h/3*2*f(X[i])
for i in range(1, N, 2): # Legger til "oddetallsindekser":
S = S + h/3*4*f(X[i])
print(f"Integralet er tilnærmet lik {S:.3f}")
Integralet er tilnærmet lik 2.000
Oppgave 5.15#
import numpy as np
import matplotlib.pyplot as plt
h = 0.01
x = np.arange(0, 4, h)
y = np.zeros(len(x))
y[0]= 2 # Initialverdien
for i in range(0, len(x)-1):
y[i + 1] = y[i] + h * (5*np.exp(-x[i])*np.cos(x[i])-y[i])
plt.plot(x, y, "b")
plt.xlabel("x")
plt.ylabel("y")
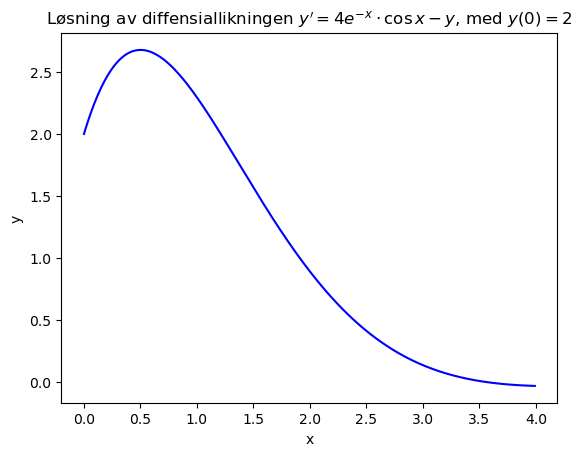
plt.title(r"Løsning av diffensiallikningen $y'=4e^{-x}\cdot \cos x -y$, med $y(0)=2$")
plt.show()
import numpy as np
import matplotlib.pyplot as plt
h = 0.01
# Beregner først verdiene større eller lik 0:
x = np.arange(0, 1.5, h)
y = np.zeros(len(x))
y[0]= 1 # Initialverdien
for i in range(0, len(x)-1):
y[i + 1] = y[i] + h * (y[i] -x[i]*np.exp(x[i]))
# Beregner så verdiene mindre enn 0:
X = list(np.arange( -4, 0+h, h)) # Må legge til h for å få med 0
Y = np.zeros(len(X))
Y[-1]= 1 # Initialverdien
# Må trokle meg baklengs gjennom lista for å få initialverdien bakerst:
for i in range(0, len(X)-1):
Y[-2-i] = Y[-1-i] -h * (Y[-1-i] -X[-1-i]*np.exp(X[-1-i]))
# Setter sammen de to listene:
x = np.concatenate((X, x))
y = np.concatenate((Y, y))
plt.plot(x, y)
#plt.plot(X, Y)
plt.xlabel("x")
plt.ylabel("y")
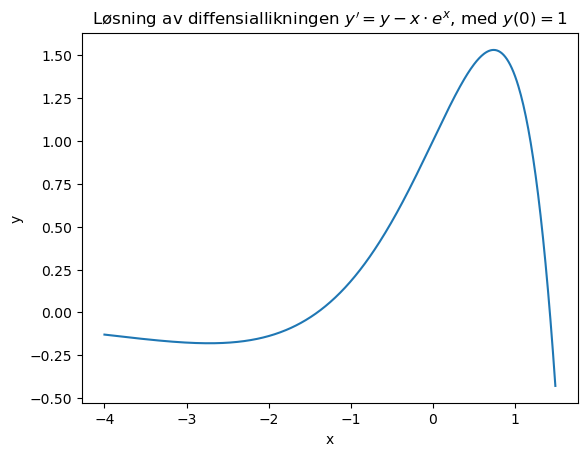
plt.title(r"Løsning av diffensiallikningen $y'=y-x\cdot e^x$, med $y(0)=1$")
plt.show()
Oppgave 5.17 c)#
import numpy as np
def f(x):
return np.exp(-x**2)-1/2
X = np.linspace(-2, 2, 10000)
for i in range(len(X)-1):
if f(X[i])*f(X[i+1]) < 0:
print(f"Nullpunkt i {(X[i]+X[i+1])/2:.3f}")
Nullpunkt i -0.832
Nullpunkt i 0.832
Oppgave 5.18#
import numpy as np
def f(x):
return np.exp(-x)
x = 1 # Startverdien for x
epsilon = 1e-10 # Nøyaktigheten vi ønsker
while abs(f(x) - x) > epsilon:
x = f(x)
print(f"{x:.10f}")
0.5671432905
Oppgave 5.19#
Jeg plotter først grafen til \(f(x)=\ln(x^2+1)-(x^2-1)\) i et koordinatsystem, slik at jeg kan se hvor det eventuelt er løsninger.
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return np.log(x**2+1)-(x**2-1)
X = np.linspace(-2, 2, 1000)
plt.plot(X, f(X)) # Plotter funksjonen
plt.grid() # Viser et rutenett
plt.show() # Viser grafen
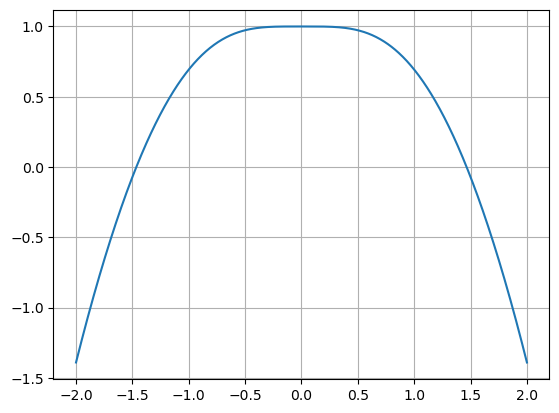
Jeg ser at det er to løsninger. En mellom -1 og 0 og en mellom 0 og 1. Jeg kan bruke halveringsmetoden for å finne disse.
def Halveringsmetoden(f, a, b, epsilon=1e-10):
""" Halveringsmetoden for å finne nullpunktet til en funksjon f(x)
i intervallet [a,b] med ønsket nøyaktighet epsilon.
"""
while b-a > epsilon:
m = (a+b)/2
if f(a)*f(m) < 0:
b = m
else:
a = m
return (a+b)/2
a =Halveringsmetoden(f, -2, -1)
b =Halveringsmetoden(f, 1, 2)
print(f"Nullpunktene er {a:.10f} og {b:.10f}")
Nullpunktene er -1.4649891538 og 1.4649891538
Oppgave 5.21#
Her kan vi ikke bruke \(f(x)=\tan x\) siden funksjonsverdiene ikke vil havne i intervallet \(\left<\frac{\pi}{2},\frac{3\pi}{2}\right>\). Vi må i stedet bruke den omvendte funksjonen \(f(x)=\arctan x\). Problemet med denne, er at den gir oss verdier mellom \(\left<-\frac{\pi}{2},\frac{\pi}{2}\right>\), og vi ønsker å finne verdier mellom \(\left<\frac{\pi}{2},\frac{3\pi}{2}\right>\). Vi kan løse dette ved å bruke \(f(x)=\pi + \arctan x\).
import numpy as np
def f(x):
return np.arctan(x)+np.pi
x = 2 # Startverdien for x
epsilon = 1e-10 # Nøyaktigheten vi ønsker
while abs(f(x) - x) > epsilon:
x = f(x)
print(f"{x:.10f}")
4.4934094579
Oppgave 5.23#
I denne oppgaven ser vi at funksjonen df er definert som endring i f(x) delt på endring i x. Dette er definisjonen på den deriverte. I stedet for å legge til en \(\Delta x\), ganger vi \(x\) med et tall \(k\) og får \(kx\). Dersom \(k\) er nær 1, vil \(\Delta x = kx-x\) være veldig liten. Endring i \(y\) verdier blir da \(\Delta y = f(kx)-f(x)\). Ut fra definisjonen til den deriverte, får vi altså at \(df\) er en tilnærming til den deriverte når \(k\) er veldig nær 1.
Oppgave 5.25#
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return (x+1)/(x**2+1)
X = np.linspace(-2, 2, 1000)
def df(x, h=0.0001):
return (f(x+h)-f(x))/h # Derivasjonen av funksjonen
def ddf(x, h=0.0001):
return (df(x+h)-df(x))/h # Andrederiverte av funksjonen
plt.plot(X, ddf(X)) # Plotter funksjonen
plt.grid() # Viser et rutenett
plt.xlabel("x")
plt.ylabel("y")
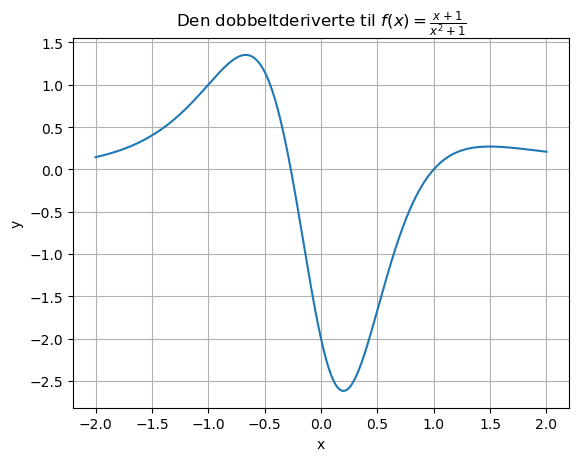
plt.title(r"Den dobbeltderiverte til $f(x)=\frac{x+1}{x^2+1}$")
plt.show() # Viser grafen
Oppgave 5.26#
import numpy as np
start = -1
slutt = 1
N = 1000
h = (slutt-start)/N # Bredden på rektanglene
def f(x):
return np.sqrt(1-x**2)
# Venstre Riemannsum:
x = start # Startverdien for x
S = 0 # Summerer rektanglene
while x < 1:
S = S + f(x)*h
x = x + h
print(f"Venstre Riemannsum er {S:.4f}")
# Høyre Riemannsum:
x = start + h # Startverdien for x
S = 0 # Summerer rektanglene
while x <= 1:
S = S + f(x)*h
x = x + h
print(f"Høyre Riemannsum er {S:.4f}")
Venstre Riemannsum er 1.5707
Høyre Riemannsum er 1.5707
Merk at dette er det samme som \(\frac{\pi}{2}\).
Oppgave 5.27#
from numpy import e
def Trapesmetoden(f, a, b, N=1000):
S = 0
h = (b - a) / N # bredden (eller "høyden") til trapesene)
x = a # Start
for i in range(N):
S += (f(x) + f(x + h)) * h / 2 # Arealet til et trapes
x += h # Går ett steg til høyre
return S
# Tester funksjonen $f(x)=1/x med a = 1 og b = e:
def f(x):
return 1/x
print(Trapesmetoden(f, 1, e))
1.0000002127429146

